10. Searching and Sorting in JS
Searching data and sorting through data are fundamental algorithms. Searching refers to iterating over the data structure’s elements to retrieve some data. Sorting refers to putting the data structure’s elements in order. The searching and sorting algorithms are different for every data structure. This chapter focuses on searching and sorting for arrays. By the end of this chapter, you will understand how to use common sorting and searching algorithms for arrays.
Searching
As mentioned, searching is the task of looking for a specific element inside a data structure. When searching in an array, there are two main techniques depending on whether the array is sorted. In this section, you’ll learn about linear and binary searching. Linear searches are especially flexible because they can be used with both sorted and unsorted data. Binary searches are specifically used with sorted data. However, a linear search has a higher time complexity than a binary search.
Linear Search
A linear search works by going through each element of the array one index after another sequentially. The following code example is an implementation of a linear search that iterates through the entire array of numbers to find out whether 4 and 5 exist within the array.
1 //iterate through the array and find
2 function linearSearch(array,n){
3 for(var i=0; i<array.length; i++) {
4 if (array[i]==n) {
5 return true;
6 }
7 }
8 return false;
9 }
10 console.log(linearSearch([1,2,3,4,5,6,7,8,9], 6)); // true
11 console.log(linearSearch([1,2,3,4,5,6,7,8,9], 10)); // false
Time Complexity: O(n)
As shown in Figure 10-1, when 6 is searched for, it goes through six iterations. When 10 is searched for, it must iterate through all n elements before returning false; therefore, the time complexity is O(n).

Figure 10-1
Linear search
As another example, with an array of [1,2,3,4,5] and a search term of 3, it would take three iterations to complete (1, 2, 3). The reason why this algorithm has a Big-O of O(n) is that, in the worst-case scenario, the entire array needs to be iterated. For example, if the search term is 5, it takes five iterations (1, 2, 3, 4, 5). If 6 is the search term, it goes through the entire array (1, 2, 3, 4, 5) and then returns false because it was not found.
As noted previously, a linear search algorithm like this is great because it works whether or not the array is sorted. In a linear search algorithm, every element of the array is checked. So, you should use a linear search when the array is not sorted. If the array is sorted, you can do the search faster via a binary search.
Binary Search
Binary search is a searching algorithm that works on sorted data. Unlike the linear search algorithm, in which every element of the array is checked, binary searches can check the middle value to see whether the desired value is greater or smaller than it. If the desired value is smaller, this algorithm can search through the smaller parts, or it can search through the bigger parts if the desired value is bigger.
Figure 10-2 illustrates the process of a binary search. First, the search range is 1 to 9. Since the middle element, 5, is bigger than 3, the search range is restricted to 1 to 4. Finally, 3 is found as the middle element. Figure 10-3 illustrates searching for an item in the right half of the array.
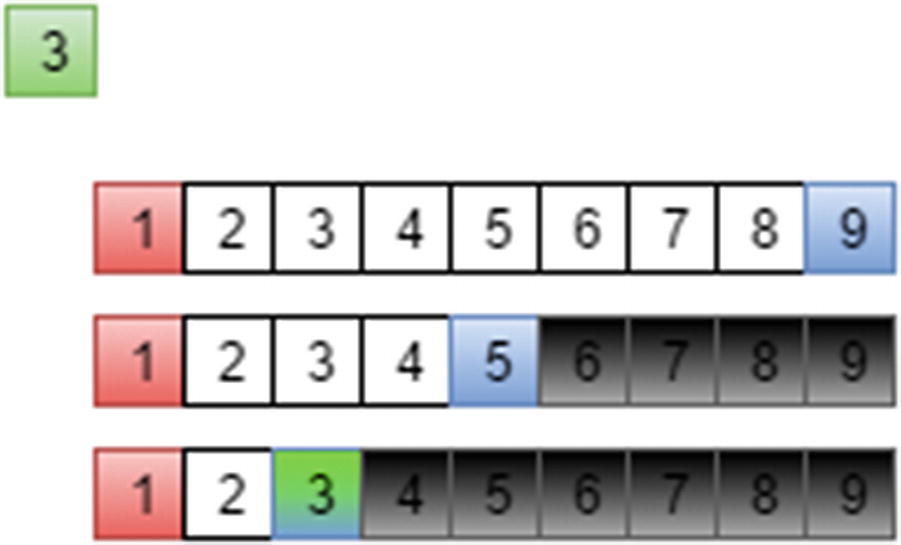
Figure 10-2
Binary search in the left half of the array
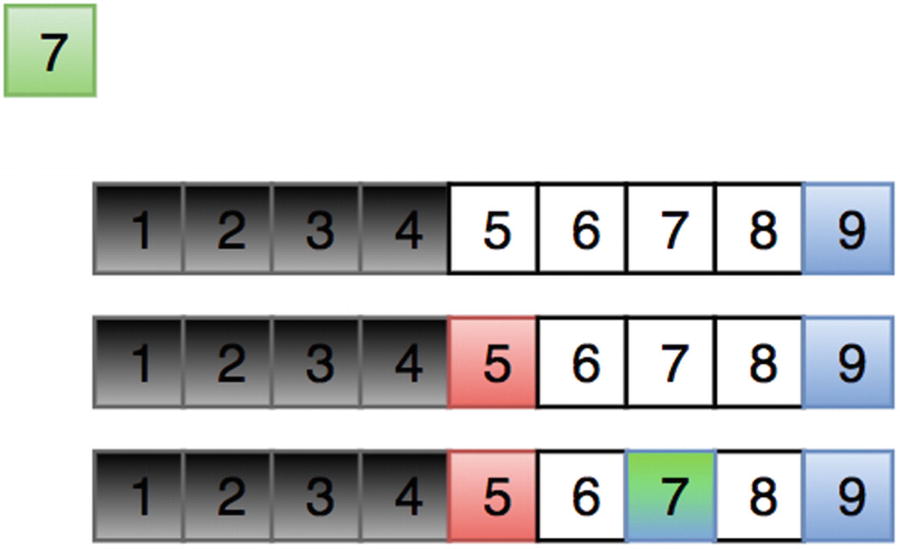
Figure 10-3
Binary search in the right half of the array
The following code implements the binary search algorithm described:
1 function binarySearch(array,n){
2 var lowIndex = 0, highIndex = array1.length-1;
3
4 while(lowIndex<=highIndex){
5 var midIndex = Math.floor((highIndex+lowIndex) /2);
6 if (array[midIndex]==n) {
7 return midIndex;
8 } else if (n>array[midIndex]) {
9 lowIndex = midIndex;
10 } else {
11 highIndex = midIndex;
12 }
13 }
14 return -1;
15 }
16 console.log(binarySearch([1,2,3,4], 4)); // true
17 console.log(binarySearch([1,2,3,4], 5)); // -1
The binary search algorithm is fast but can be done only if the array is sorted. It checks the middle element if that is the element that is being searched for. If the search element is bigger than the middle element, the lower bound is set to the middle element plus one. If the search element is less than the middle element, the higher bound is set to the middle element minus one.
This way, the algorithm is continuously dividing the array into two sections: the lower half and the upper half. If the element is smaller than the middle element, it should look for it in the lower half; if the element is bigger than the middle element, it should look for it in the upper half.
Binary searches are used by humans without them even knowing. An example is a phone directory that is arranged from A to Z by last name.
If you are given the task of finding someone with the last name of Lezer, one would first go to the L section and open it halfway through. Lizar is on that page; this means that the lower section contains L + [a to i] and the upper section contains L + [i to z] last names. You would then check the middle of the lower section. Laar appears, so you would now check the upper section. This process repeats until Lezer is found.
Sorting
Sorting is one of the most important topics in computer science; it is faster and easier to locate items in a sorted array than in an unsorted sorted array. You can use sorting algorithms to sort an array in memory for searching later in the program or to write to a file for later retrieval. In this section, different sorting techniques will be explored. We will start with the naive sorting algorithms and then explore efficient sorting algorithms. Efficient sorting algorithms have various trade-offs that should be considered during usage.
Bubble Sort
Bubble sorting is the simplest sorting algorithm. It simply iterates over the entire array and swaps elements if one is bigger than the other, as shown in Figure 10-4 and Figure 10-5.
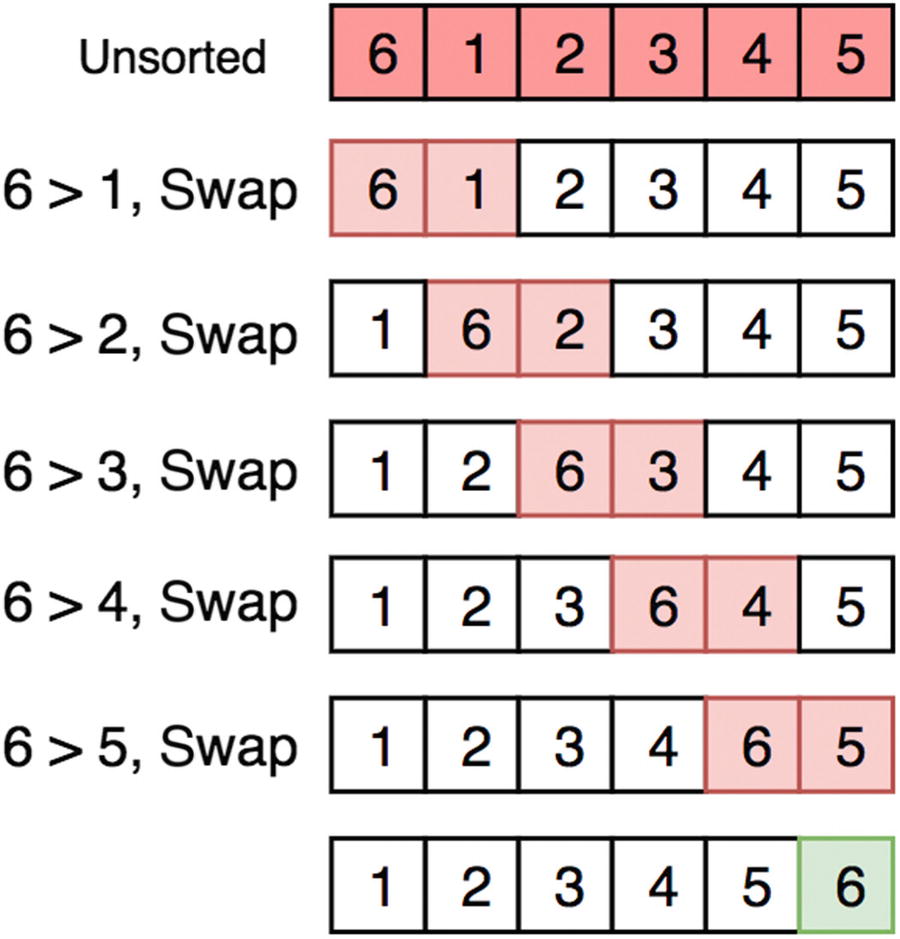
Figure 10-4
First run of the bubble sort
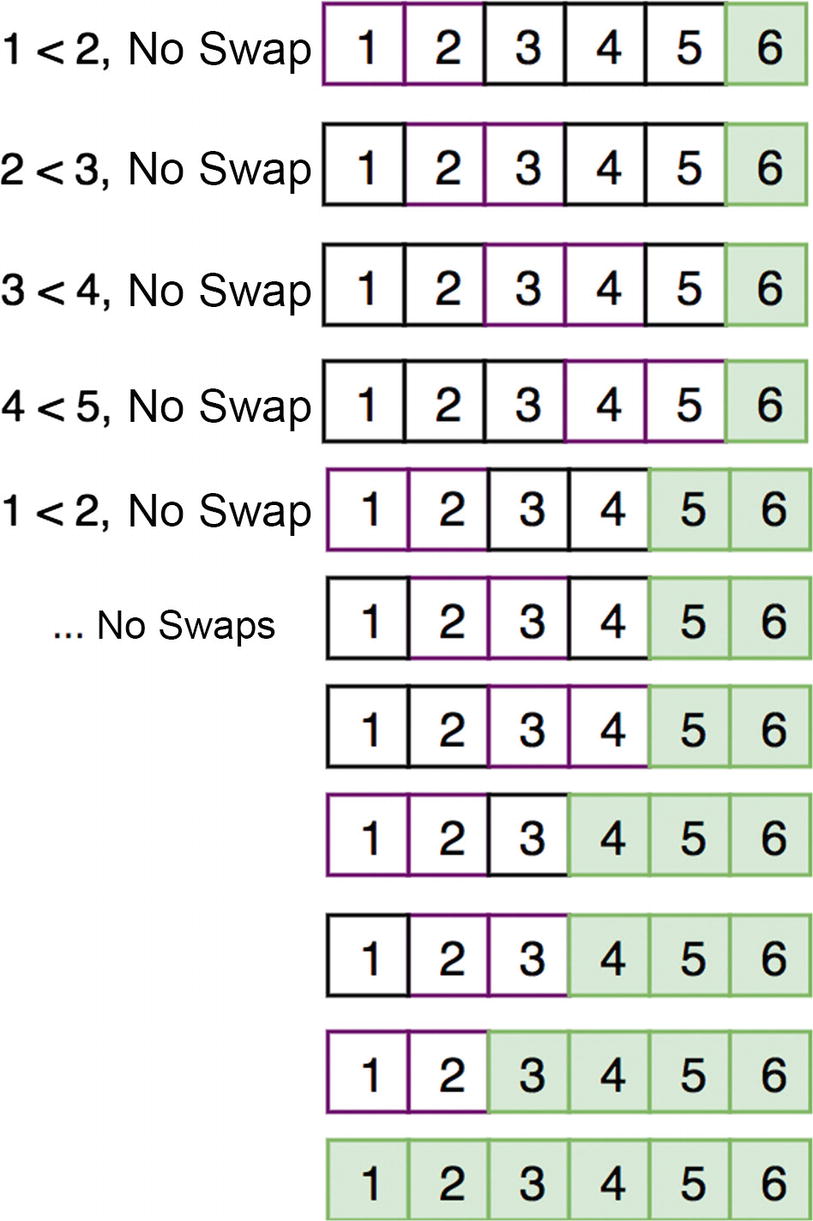
Figure 10-5
The rest of the bubble sort runs
swap is a common function used in sorting. It simply switches two array element values and will be used as a helper function for most of the sorting algorithms mentioned.
1 function swap(array, index1, index2) {
2 var temp = array[index1];
3 array[index1] = array[index2];
4 array[index2] = temp;
5 }
The following bubbleSort code block illustrates the bubble sort algorithm previously described:
1 function bubbleSort(array) {
2 for (var i=0, arrayLength = array.length; i<arrayLength; i++) {
3 for (var j=0; j<=i; j++) {
4 if (array[i] < array[j]) {
5 swap(array, i, j);
6 }
7 }
8 }
9 return array;
10 }
11 bubbleSort([6,1,2,3,4,5]); // [1,2,3,4,5,6]
Time Complexity: O(n__2)
Space Complexity: O(1)
Bubble sort is the worst type of sort because it compares every pair possible, whereas other sorting algorithms take advantage of the presorted parts of the array. Because bubble sort uses nested loops, it has a time complexity of O(n__2).
Selection Sort
Selection sorting works by scanning the elements for the smallest element and inserting it into the current position of the array. This algorithm is marginally better than bubble sort. Figure 10-6 shows this minimum selection process.
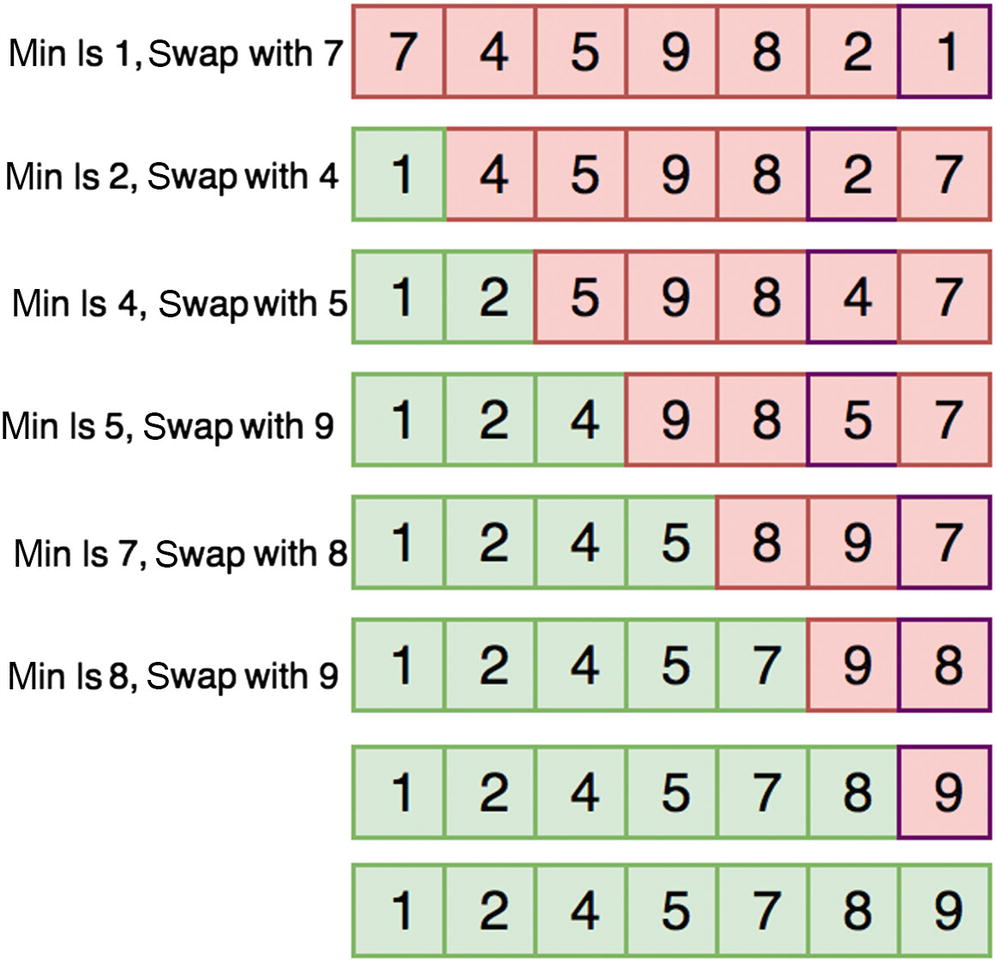
Figure 10-6
Selection sort
The following code implements the selection sort. In the code, there is one for loop to iterate through the array and one nested for loop to scan to get the minimum element.
1 function selectionSort(items) {
2 var len = items.length,
3 min;
4
5 for (var i=0; i < len; i++){
6 // set minimum to this position
7 min = i;
8 //check the rest of the array to see if anything is smaller
9 for (j=i+1; j < len; j++){
10 if (items[j] < items[min]){
11 min = j;
12 }
13 }
14 //if the minimum isn't in the position, swap it
15 if (i != min){
16 swap(items, i, min);
17 }
18 }
19
20 return items;
21 }
22 selectionSort([6,1,23,4,2,3]); // [1, 2, 3, 4, 6, 23]
Time Complexity: O(_n_2)
Space Complexity: O(1)
- The time complexity for selection sort is still O(n__2) because of the nested for loop .
Insertion Sort
Insertion sort works similarly to selection sort by searching the array sequentially and moving the unsorted items into a sorted sublist on the left side of the array. Figure 10-7 shows this process in detail.
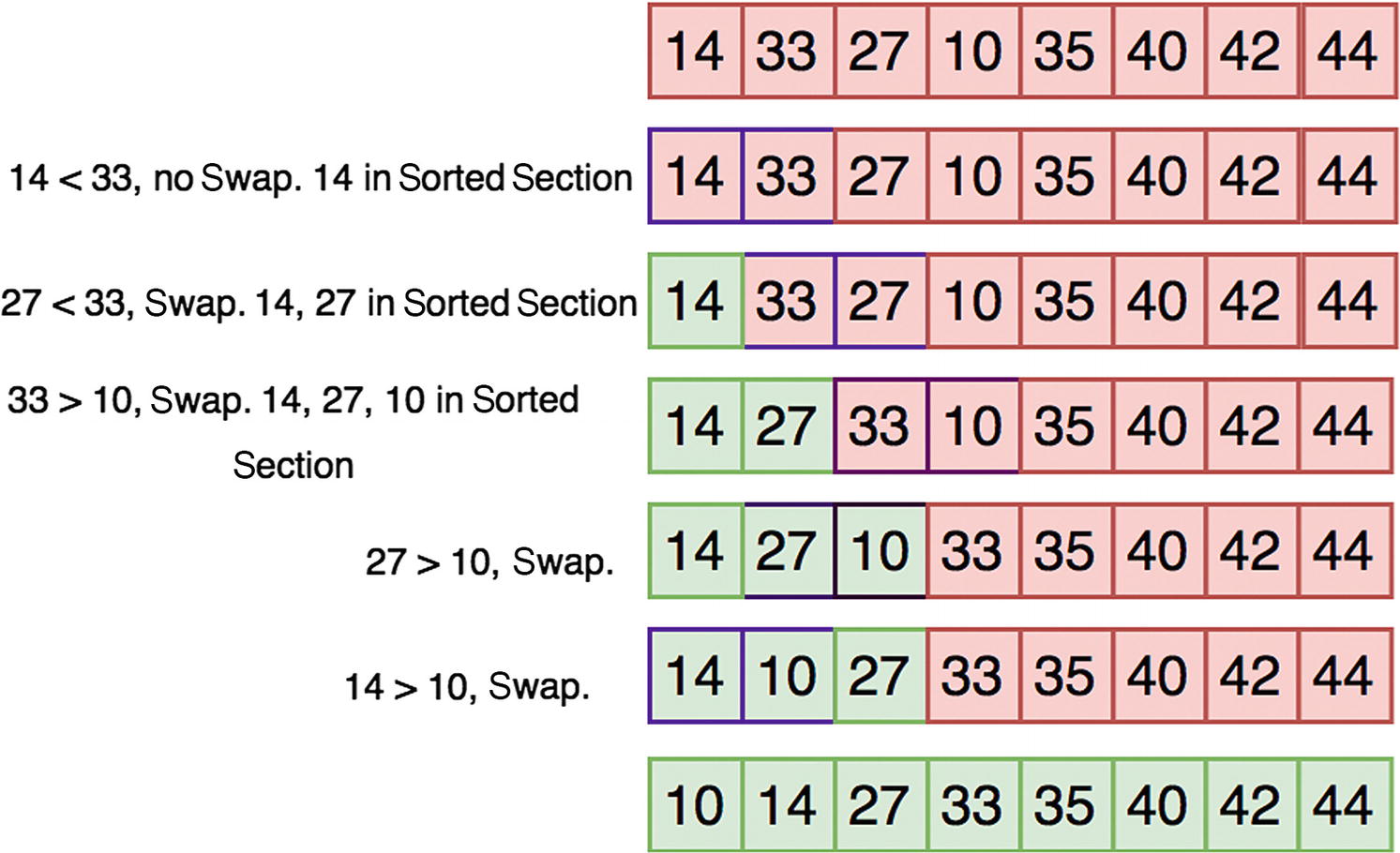
Figure 10-7
Insertion sort
The following code implements the insertion sort algorithm. The outer for loop iterates over the array indices, and the inner for loop moves the unsorted items into the sorted sublist on the left side of the array.
1 function insertionSort(items) {
2 var len = items.length, // number of items in the array
3 value, // the value currently being compared
4 i, // index into unsorted section
5 j; // index into sorted section
6
7 for (i=0; i < len; i++) {
8 // store the current value because it may shift later
9 value = items[i];
10
11 // Whenever the value in the sorted section is greater than the value
12 // in the unsorted section, shift all items in the sorted section
13 // over by one. This creates space in which to insert the value.
14
15 for (j=i-1; j > -1 && items[j] > value; j--) {
16 items[j+1] = items[j];
17 }
18 items[j+1] = value;
19 }
20 return items;
21 }
22 insertionSort([6,1,23,4,2,3]); // [1, 2, 3, 4, 6, 23]
Time Complexity: O(_n_2)
Space Complexity: O(1)
Again, this sorting algorithm has a quadratic time complexity of O(_n_2) like bubble and insertion sort because of the nested for loop.
Quicksort
Quicksort works by obtaining a pivot and partitioning the array around it (bigger elements on one side and smaller elements on the other side) until everything is sorted. The ideal pivot is the median of the array since it will partition the array evenly but getting the median of an unsorted array linear time to compute. Hence, a pivot is typically obtained by taking the median value of the first, middle, and last elements in the partition. This sort is a recursive one and uses the divide-and-conquer methodology to break the quadratic complexity barrier and get the time complexity down to O(nlog_2(_n)). However, with a pivot that partitions everything on one side, the time complexity is worse case: O(_n_2).
Figure 10-8 shows the quicksort process’s partitioning steps in great detail.
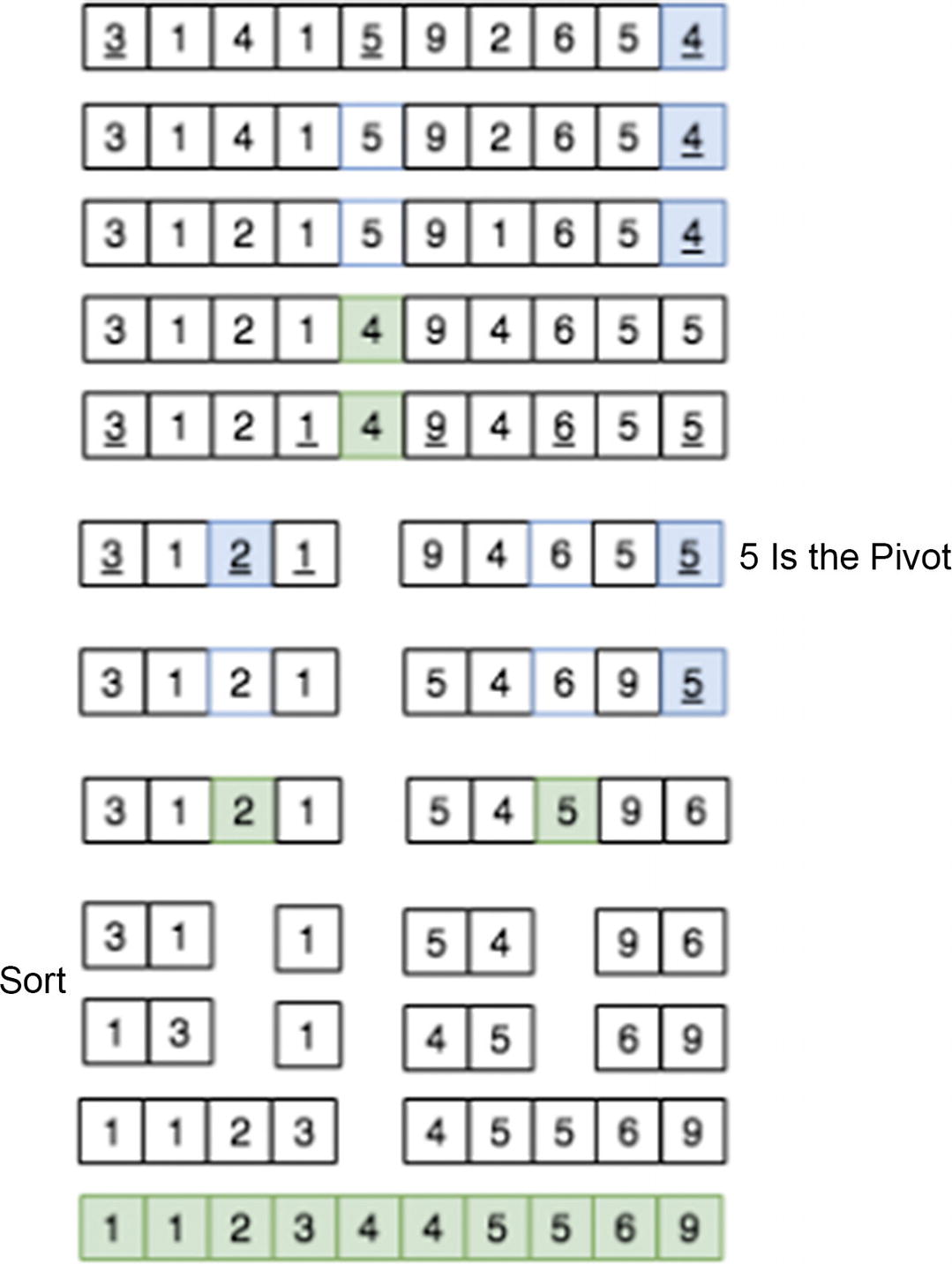
Figure 10-8
Quicksort
The following code shows an implementation of the quicksort algorithm:
1 function quickSort(items) {
2 return quickSortHelper(items, 0, items.length-1);
3 }
4
5 function quickSortHelper(items, left, right) {
6 var index;
7 if (items.length > 1) {
8 index = partition(items, left, right);
9
10 if (left < index - 1) {
11 quickSortHelper(items, left, index - 1);
12 }
13
14 if (index < right) {
15 quickSortHelper(items, index, right);
16 }
17 }
18 return items;
19 }
20
21 function partition(array, left, right) {
22 var pivot = array[Math.floor((right + left) / 2)];
23 while (left <= right) {
24 while (pivot > array[left]) {
25 left++;
26 }
27 while (pivot < array[right]) {
28 right--;
29 }
30 if (left <= right) {
31 var temp = array[left];
32 array[left] = array[right];
33 array[right]= temp;
34 left++;
35 right--;
36 }
37 }
38 return left;
39 }
40
41 quickSort([6,1,23,4,2,3]); // [1, 2, 3, 4, 6, 23]
Time Complexity: O(nlog_2(_n)) on average, O(n2) for worst case
Space Complexity: O(log_2(_n))
One downside about a quicksort algorithm is that it could potentially be O(n_2) if a bad pivot is always picked . A bad pivot is one that it does not partition the array evenly. The ideal pivot is the median element of the array. In addition, a quicksort algorithm takes a bigger space complexity of O(_log_2(_n)) compared to other sorting algorithms because of the call stack in recursion.
Use a quicksort algorithm when the average performance should be optimal. This has to do with the fact that quicksort works better for the RAM cache.
Quickselect
Quickselect is a selection algorithm to find the k_th smallest element in an unordered list. Quickselect uses the same approach as a quicksort algorithm. A pivot is chosen, and the array is partitioned. Instead of recursing both sides like quicksort, however, it recurses only the side for the element. This reduces the complexity from O(_nlog_2(_n)) to O(n).
Quickselect is implemented in the following code:
1 var array = [1,3,3,-2,3,14,7,8,1,2,2];
2 // sorted form: [-2, 1, 1, 2, 2, 3, 3, 3, 7, 8, 14]
3
4 function quickSelectInPlace(A, l, h, k){
5 var p = partition(A, l, h);
6 if(p==(k-1)) {
7 return A[p];
8 } else if(p>(k-1)) {
9 return quickSelectInPlace(A, l, p - 1,k);
10 } else {
11 return quickSelectInPlace(A, p + 1, h,k);
12 }
13 }
14
15 function medianQuickselect(array) {
16 return quickSelectInPlace(array,0,array.length-1, Math.floor(array.length/2));
17 }
18
19 quickSelectInPlace(array,0,array.length-1,5); // 2
20 // 2 - because it's the fifth smallest element
21 quickSelectInPlace(array,0,array.length-1,10); // 7
22 // 7 - because it's the tenth smallest element
Time Complexity: O(n)
Mergesort
Mergesort works by dividing the array into subarrays until each array has one element. Then, each subarray is concatenated (merged) in a sorted order (see Figure 10-9).
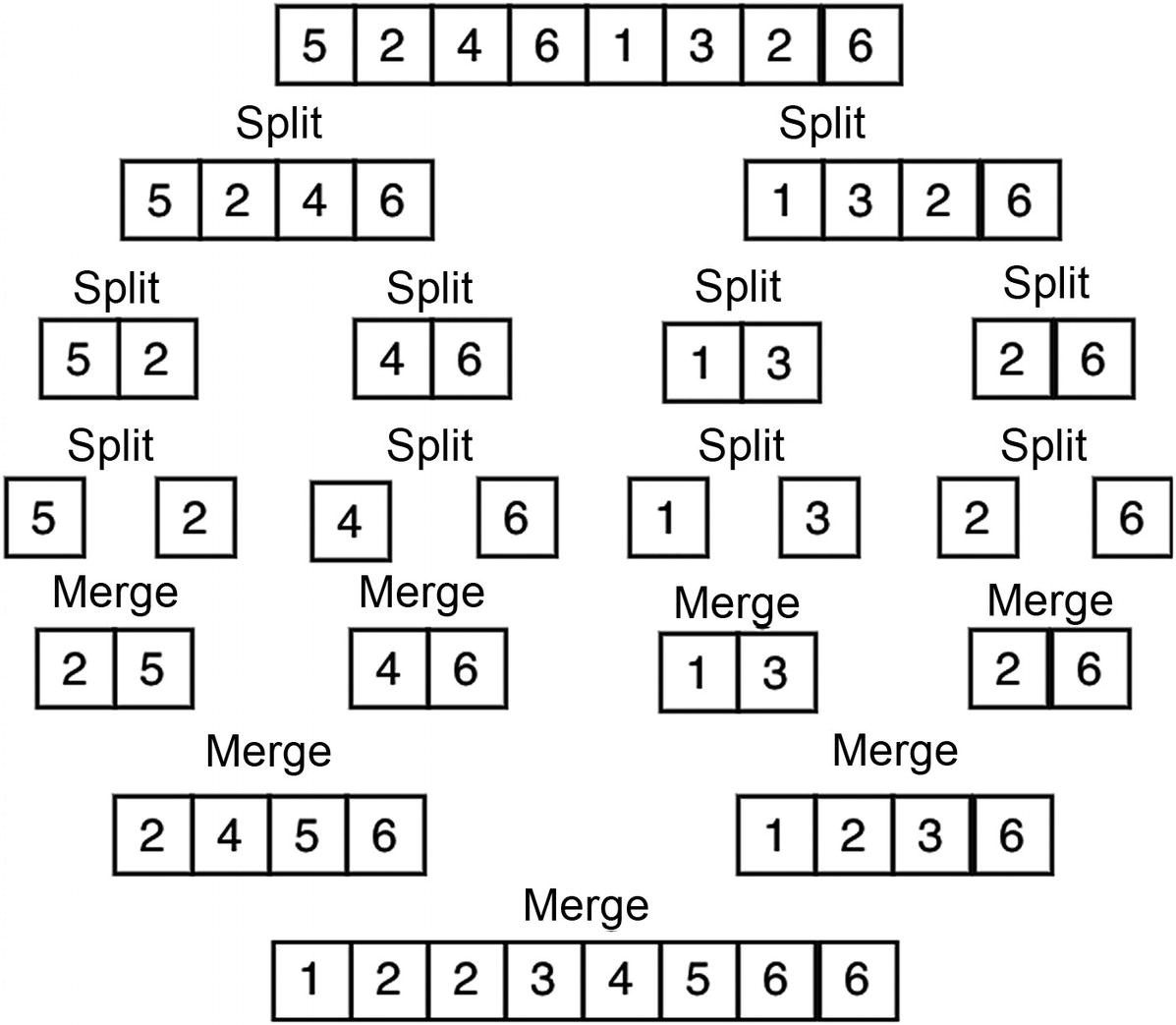
Figure 10-9
Mergesort
The merge function should add all the elements from both arrays in sorted order in a “result array.” To do this, the index of each array can be created to keep track of elements already compared. Once one array exhausts all its elements, the rest can be appended to the result array.
1 function merge(leftA, rightA){
2 var results= [], leftIndex= 0, rightIndex= 0;
3
4 while (leftIndex < leftA.length && rightIndex < rightA.length) {
5 if( leftA[leftIndex]<rightA[rightIndex] ){
6 results.push(leftA[leftIndex++]);
7 } else {
8 results.push(rightA[rightIndex++]);
9 }
10 }
11 var leftRemains = leftA.slice(leftIndex),
12 rightRemains = rightA.slice(rightIndex);
13
14 // add remaining to resultant array
15 return results.concat(leftRemains).concat(rightRemains);
16 }
The merging function works by taking the two arrays (left and right) and merging them into one resultant array. The elements need to be compared as they get merged to preserve order.
Now, the mergeSort function has to partition the bigger array into two separate arrays and recursively call merge.
1 function mergeSort(array) {
2
3 if(array.length<2){
4 return array; // Base case: array is now sorted since it's just 1 element
5 }
6
7 var midpoint = Math.floor((array.length)/2),
8 leftArray = array.slice(0, midpoint),
9 rightArray = array.slice(midpoint);
10
11 return merge(mergeSort(leftArray), mergeSort(rightArray));
12 }
13 mergeSort([6,1,23,4,2,3]); // [1, 2, 3, 4, 6, 23]
Time Complexity: O(nlog_2(_n))
Space Complexity: O(n)
Mergesort has a large space complexity of O(n) because of the need to create n number of arrays to be merged later. Use mergesort when a stable sort is needed. A stable sort is one that’s guaranteed not to reorder elements with identical keys. Mergesort is guaranteed to be O(nlog__2__(n)). A disadvantage of mergesort is that it uses O(n) in space.
Count Sort
Count sort can be done in O(k+n) because it does not compare values. It works only for numbers and given a certain range. Instead of sorting by swapping elements, this count works by counting occurrences of each element in the array. Once occurrences of each element are counted, the new array can be created using those occurrences. This sorts the data without having to swap elements, as shown in Figure 10-10.
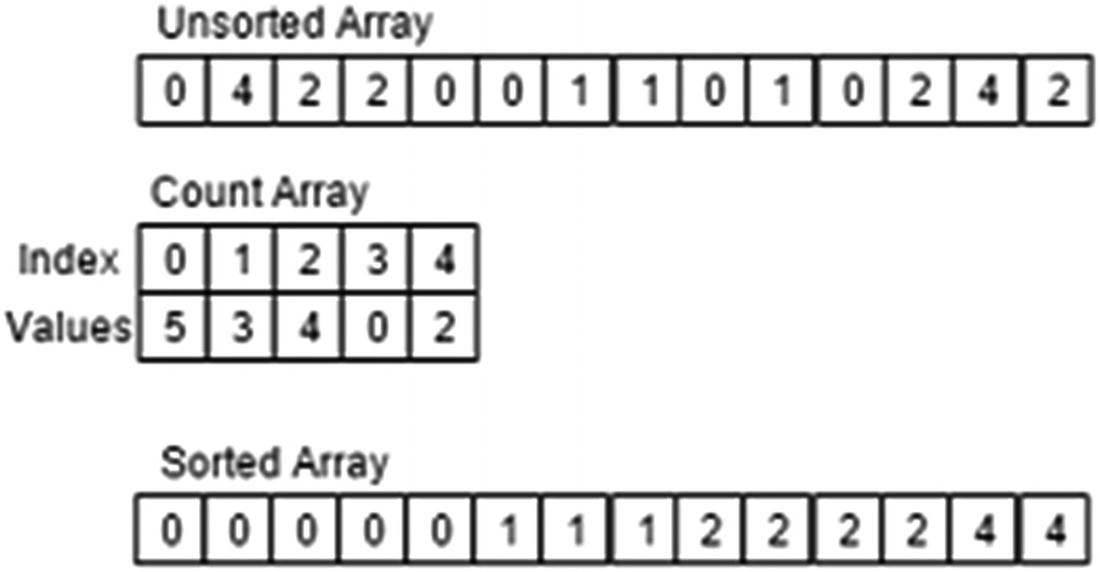
Figure 10-10
Count sort
Here’s an implementation using a JavaScript object:
1 function countSort(array) {
2 var hash = {}, countArr= [];
3 for(var i=0;i<array.length;i++){
4 if(!hash[array[i]]){
5 hash[array[i]] = 1;
6 }else{
7 hash[array[i]]++;
8 }
9 }
10
11 for(var key in hash){
12 // for any number of _ element, add it to array
13 for(var i=0;i<hash[key];i++) {
14 countArr.push(parseInt(key));
15 }
16 }
17
18 return countArr;
19 }
20 countSort([6,1,23,2,3,2,1,2,2,3,3,1,123,123,4,2,3]); // [1, 2, 3, 4, 6, 23]
Time Complexity: O(k+n)
Space Complexity: O(k)
Use count sort when you’re sorting integers with a limited range. This will be the fastest sort for this case.
JavaScript’s Built-in Sort
JavaScript has a built-in sort() method for an array object, which sorts elements by ascending order. To use it, there is an optional parameter that you can pass in a comparator function.
However, the default comparator function sorts alphabetically, so it will not work for numbers.
1 var array1 = [12,3,4,2,1,34,23];
2 array1.sort(); // array1: [1, 12, 2, 23, 3, 34, 4]
In the previous example, notice that numbers starting with 1 came first (1, 12), then numbers starting with 2, and so forth. This is because no comparator function was passed and JavaScript converted the elements into a string and sorted it according to the alphabet.
To sort numbers correctly, use this:
1 var array1 = [12,3,4,2,1,34,23];
2
3 function comparatorNumber(a,b) {
4 return a-b;
5 }
6
7 array1.sort(comparatorNumber);
8 // array1: [1, 2, 3, 4, 12, 23, 34]
a-b indicates that it should be from smallest to biggest (ascending). Descending order can be done as follows:
1 var array1 = [12,3,4,2,1,34,23];
2
3 function comparatorNumber(a,b) {
4 return b-a;
5 }
6
7 array1.sort(comparatorNumber); // array1: [34, 23, 12, 4, 3, 2, 1]
The sort() function can be useful when you need a quick way to sort something without implementing it yourself.
Summary
There are two ways to search inside an array: linear search and binary search. Binary search is faster with O(log_2(_n)) time complexity, while linear search has O(n) time complexity. However, the binary search can be performed only on a sorted array.
Table 10-1 summarizes time and space complexities of different sorting algorithms. The most efficient sorting algorithms are quicksort, mergesort, and count sort. Count sort, while the fastest, is limited to when the range of array’s values are known.
Table 10-1
Sorting Summary
Algorithm
Time Complexity
Space Complexity
Quicksort
O(nlog_2(_n))
O(nlog_2(_n))
Mergesort
O(nlog_2(_n))
O(nlog_2(_n))
Bubble sort
O(_n_2)
O(_n_2)
Insertion sort
O(_n_2)
O(_n_2)
Selection sort
O(_n_2)
O(_n_2)
Count sort
O(k + n)
O(k)
Exercises
USE THE IMPLEMENT SQUARE ROOT FUNCTION FOR AN INTEGER WITHOUT USING ANY MATH LIBRARIES
The first solution that may come to mind is trying every possibility from 1 to the number, as follows:
1 function sqrtIntNaive(number){
2 if(number == 0 || number == 1)
3 return number;
4
5 var index = 1, square = 1;
6
7 while(square < number){
8 if (square == number){
9 return square;
10 }
11
12 index++;
13 square = index*index;
14 }
15 return index;
16 }
17 sqrtIntNaive(9);
Time Complexity: O(n)
This is essentially a linear search since it has to linearly check one by one the value for the square root.
The binary search algorithm can be applied to this problem. Instead of going up 1 by 1, partition the range into upper half and lower half between 1 and the given number as follows:
1 function sqrtInt(number) {
2 if(number == 0 || number == 1) return number;
3
4 var start = 1, end = number, ans;
5
6 while(start <= end) {
7 let mid = parseInt((start+end)/2);
8
9 if (mid*mid == number)
10 return mid;
11
12 if(mid*mid<number){
13 start = mid+1; // use the upper section
14 ans = mid;
15 }else{
16 end = mid-1; // use the lower section
17 }
18 }
19 return ans;
20 }
21 sqrtInt(9);
Time Complexity: O(log_2(_n))
Bonus: Find a Square Root of a Float
For this exercise, the only difference is using a threshold value to calculate accuracy to because the square root of a double will have decimals. Hence, the time complexity also stays the same.
1 function sqrtDouble(number) {
2 var threshold = 0.1;
3 //9 try middle,
4 var upper = number;
5 var lower = 0;
6 var middle;
7 while(upper-lower>threshold){
8 middle = (upper+lower)/2;
9 if(middle*middle>number){
10 upper = middle;
11 }else{
12 lower = middle;
13 }
14 }
15 return middle
16 }
17 sqrtDouble(9); // 3.0234375
FIND IF TWO ELEMENTS OF AN ARRAY ADD UP TO A GIVEN NUMBER
The simple approach to this problem is to check every other element for each element in the array.
1 function findTwoSum(array, sum) {
2
3 for(var i=0, arrayLength = array.length; i<arrayLength;i++){
4 for(var j=i+1;j<arrayLength;j++){
5 if(array[j]+array[i] == sum){
6 return true;
7 }
8 }
9 }
10 return false;
11 }
Time Complexity: O(_n_2)
Space Complexity: O(1)
There is a lot of checking, and hence it takes quadratic time.
A better approach is to store the already visited numbers and check against them. This way, it can be done in linear time.
1 function findTwoSum(array, sum){
2 var store = {};
3
4 for(var i=0, arrayLength = array.length; i<arrayLength;i++){
5 if(store[array[i]]){
6 return true;
7 }else{
8 store[sum-array[i]] = array[i];
9 }
10 }
11 return false;
12 }
Time Complexity: O(n)
Space Complexity: O(n)
This algorithm cuts the time complexity to O(n) but takes O(n) space as well to store items into the store object.
FIND AN ELEMENT WITHIN AN ARRAY THAT APPEARS ONLY ONCE
Given a sorted array in which all elements appear twice (one after one) and one element appears only once, find that element in O(l_og__2__n_) complexity. This can be done by modifying the binary search algorithm and checking the addition indices.
Input: arr = [1, 1, 3, 3, 4, 5, 5, 7, 7, 8, 8] Output: 4
Input: arr = [1, 1, 3, 3, 4, 4, 5, 5, 7, 7, 8] Output: 8
1 function findOnlyOnce(arr, low, high) {
2 if (low > high) {
3 return null;
4 }
5 if (low == high) {
6 return arr[low];
7 }
8
9 var mid = Math.floor((high+low)/2);
10
11 if (mid%2 == 0) {
12 if (arr[mid] == arr[mid+1]) {
13 return findOnlyOnce(arr, mid+2, high);
14 } else {
15 return findOnlyOnce(arr, low, mid);
16 }
17 } else {
18 if (arr[mid] == arr[mid-1]) {
19 return findOnlyOnce(arr, mid+1, high);
20 } else {
21 return findOnlyOnce(arr, low, mid-1);
22 }
23 }
24 }
25 function findOnlyOnceHelper(arr) {
26 return findOnlyOnce(arr, 0, arr.length);
27 }
28 findOnlyOnceHelper([ 1, 1, 2, 4, 4, 5, 5, 6, 6 ]);
Time Complexity: O(log2_n_)
Space Complexity: O(1)
CREATE A JAVASCRIPT SORT COMPARATOR FUNCTION THAT WOULD SORT STRING BY LENGTH
This is fairly simple. If it is an array of strings, strings all have a property of length, which can be used to sort the array.
1 var mythical = ['dragon', 'slayer','magic','wizard of oz', 'ned stark'];
2
3 function sortComparator(a,b){
4 return a.length - b.length;
5 }
6 mythical.sort(sortComparator);
7 // ["magic", "dragon", "slayer", "ned stark", "wizard of of"]
Examples
Sort string elements, putting strings with a first, as shown here:
1 var mythical = ['dragon', 'slayer','magic','wizard of oz', 'ned tark'];
2
3 function sortComparator(a,b){
4 return a.indexOf("a") - b.indexOf("a");
5 }
6
7 mythical.sort(sortComparator);
8 // ["magic", "dragon", "slayer", "wizard of oz", "ned stark"]
Sort object elements by the number of properties, as shown here:
1 var mythical=[{prop1:", prop2:"},{prop1:", prop2:", prop3:"},{prop1:", prop2:"}];
2
3 function sortComparator(a,b){
4 return Object.keys(a).length - Object.keys(b).length;
5 }
6
7 mythical.sort(sortComparator);
// [{prop1:", prop2:"},{prop1:", prop2:"},{prop1:", prop2:", prop3:"}]
As shown, there’s a lot of flexibility with these comparators, and they can be used for sorting without needing to implement a sort yourself.
IMPLEMENT A WORD COUNTER LIST
Create a function that generates an object of words (as keys) and the number of times the words occur in a string ordered by highest to lowest occurrences.
Here’s some example input: practice makes perfect. get perfect by practice. just practice.
Here’s the example output: { practice: 3, perfect: 2, makes: 1, get: 1, by: 1, just: 1 }.
1 function wordCount(sentence) {
2 // period with nothing so it doesn't count as word
3 var wordsArray = sentence.replace(/[.]/g,"").split(" "),
4 occurenceList = {}, answerList = {};
5
6 for (var i=0, wordsLength=wordsArray.length; i<wordsLength; i++) {
7 var currentWord = wordsArray[i];
8 // doesn't exist, set as 1st occurrence
9 if (!occurenceList[currentWord]) {
10 occurenceList[currentWord] = 1;
11 } else {
12 occurenceList[currentWord]++; // add occurrences
13 }
14 }
15
16 var arrayTemp = [];
17 // push the value and key as fixed array
18 for (var prop in occurenceList) {
19 arrayTemp.push([occurenceList[prop], prop]);
20 }
21
22 function sortcomp(a, b) {
23 return b[0] - a[0]; // compare the first element of the array
24 }
25
26 arrayTemp.sort(sortcomp); //sort
27
28 for (var i = 0, arrlength = arrayTemp.length; i < arrlength; i++) {
29 var current = arrayTemp[i];
30 answerList[current[1]] = current[0]; // key value pairs
31 }
32 return answerList;
33 }
34 wordCount("practice makes perfect. get perfect by practice. just practice");
Time Complexity: O(nlog_2(_n))
Space Complexity: O(n)
Time complexity is limited by the sorting algorithm that the JavaScript engine uses. Most use either mergesort or quicksort, which are both O(nlog_2(_n)).